The field of generative modeling has witnessed remarkable advancements with the advent of diffusion models, which have set new standards in image, audio, and video generation.
However, a significant bottleneck has been the computational cost and time required for sampling high-quality data. In a recent paper titled “Simplifying, Stabilizing & Scaling Continuous-Time Consistency Models”, researchers Cheng Lu and Yang Song from OpenAI introduce innovative techniques to address these challenges.
By stabilizing continuous-time consistency models (sCMs), they achieve state-of-the-art performance with significantly reduced sampling steps, paving the way for faster and more efficient generative models.

To fully appreciate the contributions of this research, it’s essential to understand the foundational concepts involved.

Random Noise: In generative modeling, the process often begins with sampling from a simple noise distribution, typically a Gaussian distribution. This noise acts as the starting point for generating complex data samples through learned transformations.
Stochastic Processes: These are processes that evolve over time with inherent randomness. In the context of diffusion models, the forward diffusion process adds noise to data over time, forming a stochastic process.
Forward Diffusion Process: This process gradually corrupts the data (x0) by adding noise at each timestep (t), resulting in a sequence of increasingly noisy data (xt).
Reverse Diffusion Process: The generative model learns to reverse this process by denoising (xt) back to (x0) through a series of steps, effectively sampling from the data distribution.
Score-Based Models: These models estimate the gradient of the log probability density function (the “score”) to guide the reverse diffusion process.
Limitations: Diffusion models typically require hundreds of sequential steps to generate high-quality samples, making them computationally expensive and slow in practice.
Objective: CMs aim to accelerate the sampling process by learning a direct mapping from noisy inputs (xt) to clean data (x0), reducing the number of required steps.
Consistency Training (CT): CMs can be trained from scratch to produce consistent outputs across different noise levels by minimizing a consistency loss between model outputs at different times.
Consistency Distillation (CD): Alternatively, CMs can be trained by distilling knowledge from a pre-trained diffusion model, learning to approximate the behavior of the teacher model in fewer steps.
Challenges: Prior CMs have been primarily discrete-time models, which introduce discretization errors and require careful timestep scheduling. Continuous-time CMs theoretically address these issues but have suffered from training instability.
Neural ODEs: These models define continuous-time dynamics of data transformations using differential equations parameterized by neural networks.
Probability Flow ODE (PF-ODE): In diffusion models, the stochastic reverse diffusion process can be associated with a deterministic ODE that transports the noise distribution back to the data distribution.
Advantages: ODE formulations allow for continuous-time modeling and can enable exact likelihood computation under certain conditions.
Purpose: TrigFlow is introduced to unify and simplify the formulations of diffusion models and consistency models, leveraging trigonometric functions for parameterization.
Key Idea: By representing the diffusion process using sine and cosine functions, TrigFlow provides a stable and elegant framework for continuous-time modeling.
Benefits: This formulation helps identify and mitigate the sources of instability in continuous-time CMs, leading to improved training and sampling performance.
Time Embeddings: Neural networks often require time information to be embedded in a way that the model can utilize effectively. Common methods include positional embeddings and Fourier features.
Time Conditioning: Proper conditioning on time (or noise level) is crucial for models to generalize across different noise levels and ensure consistent outputs.
Group Normalization: A normalization technique that divides channels into groups and normalizes within each group, which can stabilize training.
Adaptive Group Normalization: Extends group normalization by allowing the scaling and shifting parameters to be conditioned on additional inputs, such as time embeddings.
The researchers’ approach involves a combination of theoretical insights and practical techniques to stabilize and scale continuous-time consistency models.

TrigFlow provides a new parameterization of the diffusion process using trigonometric functions, leading to simplified and stable formulations.


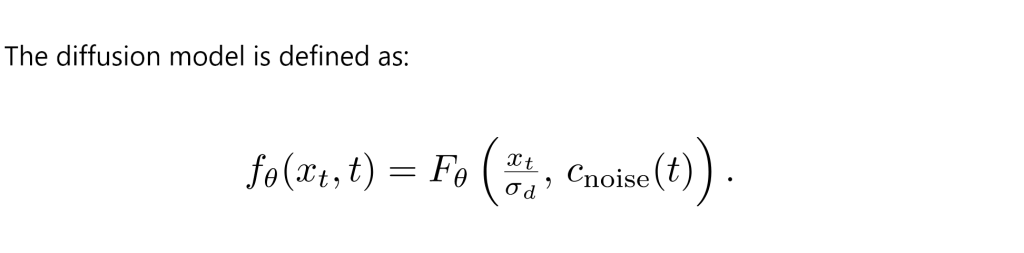

Training continuous-time CMs requires careful handling of certain components to prevent instability.
The instability primarily arises from the time derivative term in the tangent function:
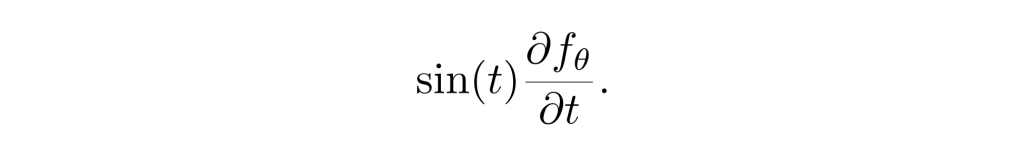
To stabilize this term, the researchers:
Initially, the time transformation is set as Cnoise(t)=t. However, to improve stability, the researchers consider alternative transformations that better capture the relationship between time and noise levels.
By incorporating adaptive group normalization conditioned on the time embeddings, the network can more effectively handle variations in the data distribution across different noise levels.
The training process involves progressively adjusting the weighting of different components in the loss function:
Adaptive Weighting: The loss terms are weighted to balance their contributions during training, preventing any single term from causing instability.
Progressive Annealing: Certain loss components are gradually increased or decreased over the course of training to guide the model towards stable convergence.

The consistency training objective minimizes the difference between the model’s outputs at different times:
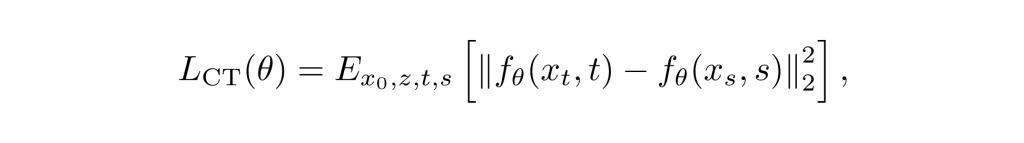
where (t) and (s) are different times sampled from the time interval, and (xt) and (xs) are the corresponding noisy samples.
Compute Per Iteration: The compute per training iteration for stabilized Consistency Distillation (sCD) is approximately twice that of the teacher diffusion model.Convergence Speed: Despite the increased per-iteration cost, sCMs converge rapidly, achieving high-quality results in a fraction of the total compute required by the teacher model.Sample Efficiency: High-quality samples can be generated after as few as 20,000 fine-tuning iterations.
The researchers conducted extensive experiments to evaluate the performance of sCMs across various datasets and settings.

Fréchet Inception Distance (FID): A standard metric for evaluating the quality of generated images by measuring the distance between the distributions of generated and real images.
Sampling Steps: The number of steps required to generate a sample from the model.
FID Score: Achieved an FID of 2.06 using two-step sampling.
Comparison: This performance is competitive with state-of-the-art diffusion models that require significantly more sampling steps.
FID Score: Achieved an FID of 1.48 with two-step sampling.
Compute Efficiency: Required less training compute compared to diffusion models while maintaining sample quality.
Model Size: Trained a model with 1.5 billion parameters.
FID Score: Achieved an FID of 1.88 using two-step sampling.
Scalability: Demonstrated that sCMs can scale to high-resolution image generation while maintaining efficiency.

Scaling Law:
Observed that increasing the model size from 200 million to 1.5 billion parameters improved the FID score by approximately 15% across datasets.
Implication:
sCMs benefit from larger model capacities, and further improvements are possible with increased compute.
Performance: CT models perform well on smaller datasets but struggle with larger, high-resolution datasets due to instability.
Limitation: Training from scratch without a teacher model can be challenging for complex data distributions.
Stability: CD models are more stable as they leverage a pre-trained diffusion model.
Efficiency: sCMs trained via CD match the sample quality of the teacher model with significantly fewer sampling steps and reduced compute.
Sampling Steps: Diffusion models typically require 50–200 steps for high-quality generation.
Comparison: sCMs achieve similar or better performance with only two sampling steps, offering substantial speedups.
Fast Sampling: Enables real-time generation of high-quality images, which is critical for applications like video generation and interactive media.
Compute Efficiency: Reduces both training and inference costs, making it feasible to deploy powerful generative models on devices with limited computational resources.
Simplified Training: The unified framework simplifies the training process, potentially reducing the need for extensive hyperparameter tuning.
Interactive Content Creation: Artists and designers can leverage sCMs for instant generation of assets, enhancing creativity and productivity.
Gaming and Virtual Reality: Real-time generation of complex environments and characters can revolutionize user experiences.
Edge Computing: Deployment on mobile devices and IoT devices becomes practical due to reduced computational demands.
Model Compression and Pruning: Further research into compressing sCMs without significant loss in quality could enhance deployability.
Multi-Modality Extensions: Extending sCMs to handle text-to-image generation, audio synthesis, or multi-modal data could open new frontiers.
Understanding Theoretical Limits: Investigating the theoretical foundations of sCMs could lead to new insights and further improvements in model design.
The work by Cheng Lu and Yang Song represents a significant advancement in generative modeling. By addressing the stability issues inherent in continuous-time consistency models, they have unlocked the potential for fast, efficient, and high-quality generation with minimal sampling steps. The introduction of the TrigFlow framework not only unifies existing methodologies but also provides practical tools for scaling and stabilizing these models. As the field progresses, stabilized continuous-time consistency models are poised to play a pivotal role in the next generation of generative AI applications, offering exciting possibilities for both research and industry.
